(Algorithm)플로이드 워셜( Floyd-Warshall Algorithm)
플로이드 워셜 알고리즘은 그래프에서 모든 꼭지점의 최단 거리를 구하는 알고리즘 이다.
음수 가중치를 갖는 변도 순환만 없다면 잘 처리된다.(다익스트라는 음수 가중치를 처리 할 수 없다)
제일 바깥문은 거쳐가는 꼭지점이고 두번째 반복문은 출발하는 꼭지점,세번째 반복문은 도착하는 꼭지점.
플로이드-워셜 알고리즘은 동적계획법 접근으로, 그래프상의 모든 두 정점을 잇는 경로의 최소 비용을 계산한다. 여기에 경유지를 기록하면 최소비용 경로까지 구할 수 있다.
다음과 같은 접근으로 설계되었다.
<Pseudo Code>
procedure floyd-warshall(두 정점을 잇는 모서리의 가중치 테이블 W)
D: 두 정점을 잇는 경로의 최소 비용 테이블, 모든 성분을 ∞로 초기화
M: 두 정점을 지나가는 최소 비용 경로가 거쳐야 할 마지막 경유지 테이블, 모든 성분을 null로 초기화
for i from 1 to [v]
for j from 1 to [v]
D[i][j]:=W[i][j]
//자기 자신은 0으로 둠
for v from 1 to [v]
D[v][v]:=0
for k from 1 to [v]
for i from 1 to [v] //출발지
for j from 1 to [v] //도착지
if D[i][j]>D[i][k]+D[k][j] // K노드의 경유지를 지났을 때 비교
D[i][j]:=D[i][k]+D[k][j]
M[i][j]:=l
return D
이렇게 구한 비용과 경유지를 활용하여 경로를 복구하는 알고리즘은 다음과 같다.
procedure floyd-warshall-path(정점 V1, 정점 V2, 경유지 테이블M)
S:경로르 역으로 저장하는 스택
P: 경로
S.push(V2);
while M[ V1 ][S.top()]
S.push(M[V1][S.top()])
while ~S.empty()
P.add(S.top());
S.pop()
return P
public static void main(String[] args) {
// TODO Auto-generated method stub
int INF=999;
int D[][]=new int[N][N];
int M[][]=new int[N][N];
int W[][]=new int[N][N];
//D를 무한대로 입력
for(int row[]:D)
Arrays.fill(row, 999);
int i,j,k;
W=new int[][]{
{0,3,1,999,999},
{3,0,999,999,999},
{1,999,0,2,999},
{999,999,2,0,2},
{999,999,999,2,0}
};
for(i=0;i<N;i++)
{
for(j=0;j<N;j++){
D[i][j]=W[i][j];
}
}
for(i=0;i<N;i++)
{
for(j=0;j<N;j++)
{
for(k=0;k<N;k++){
if(D[j][k]>D[j][i]+D[i][k]){
D[j][k]=D[j][i]+D[i][k];
M[j][k]=i;
}
}
}
}
}
private static String floyd_warshall_path(int v1,int v2,int M[][])
{
Stack<Integer> S=new Stack<Integer>();
S.push(v2);
String P="";
while(M[v1][S.peek()]!=-1){
S.push(M[v1][S.peek()]);
}
while(!S.isEmpty())
{
P+=Integer.toString(S.peek());
S.pop();
}
return P;
}
음수 가중치를 갖는 변도 순환만 없다면 잘 처리된다.(다익스트라는 음수 가중치를 처리 할 수 없다)
제일 바깥문은 거쳐가는 꼭지점이고 두번째 반복문은 출발하는 꼭지점,세번째 반복문은 도착하는 꼭지점.
플로이드-워셜 알고리즘은 동적계획법 접근으로, 그래프상의 모든 두 정점을 잇는 경로의 최소 비용을 계산한다. 여기에 경유지를 기록하면 최소비용 경로까지 구할 수 있다.
다음과 같은 접근으로 설계되었다.
- 두 정점을 잇는 최소 비용 경로는 경유지를 거치거나 거치지 않는 경로 중 하나에 속한다.
- 만약 경유지를 거친다면 그것을 이루는 부분 경로 역시 최소 비용 경로여야 한다.
<Pseudo Code>
procedure floyd-warshall(두 정점을 잇는 모서리의 가중치 테이블 W)
D: 두 정점을 잇는 경로의 최소 비용 테이블, 모든 성분을 ∞로 초기화
M: 두 정점을 지나가는 최소 비용 경로가 거쳐야 할 마지막 경유지 테이블, 모든 성분을 null로 초기화
for i from 1 to [v]
for j from 1 to [v]
D[i][j]:=W[i][j]
//자기 자신은 0으로 둠
for v from 1 to [v]
D[v][v]:=0
for k from 1 to [v]
for i from 1 to [v] //출발지
for j from 1 to [v] //도착지
if D[i][j]>D[i][k]+D[k][j] // K노드의 경유지를 지났을 때 비교
D[i][j]:=D[i][k]+D[k][j]
M[i][j]:=l
return D
이렇게 구한 비용과 경유지를 활용하여 경로를 복구하는 알고리즘은 다음과 같다.
procedure floyd-warshall-path(정점 V1, 정점 V2, 경유지 테이블M)
S:경로르 역으로 저장하는 스택
P: 경로
S.push(V2);
while M[ V1 ][S.top()]
S.push(M[V1][S.top()])
while ~S.empty()
P.add(S.top());
S.pop()
return P
계산 복잡도[편집]
플로이드-워셜 알고리즘으로 모든 정점 간 경로의 최소비용을 구하는 것은 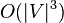 의 시간 복잡도를 갖는다. 경유지를 기록한 경우, 경로를 역으로 추출하는 알고리즘의 복잡도는
의 시간 복잡도를 갖는다. 경유지를 기록한 경우, 경로를 역으로 추출하는 알고리즘의 복잡도는  의 시간 복잡도를 갖는다. 종종 데이크스트라 알고리즘과 자주 비교되곤 하는데, 두 알고리즘 모두 각각의 장단점이 있기 때문에 상황에 맞는 알고리즘 선정 필요성이 요구된다.
의 시간 복잡도를 갖는다. 종종 데이크스트라 알고리즘과 자주 비교되곤 하는데, 두 알고리즘 모두 각각의 장단점이 있기 때문에 상황에 맞는 알고리즘 선정 필요성이 요구된다.
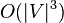 의 시간 복잡도를 갖는다. 경유지를 기록한 경우, 경로를 역으로 추출하는 알고리즘의 복잡도는
의 시간 복잡도를 갖는다. 경유지를 기록한 경우, 경로를 역으로 추출하는 알고리즘의 복잡도는  의 시간 복잡도를 갖는다. 종종 데이크스트라 알고리즘과 자주 비교되곤 하는데, 두 알고리즘 모두 각각의 장단점이 있기 때문에 상황에 맞는 알고리즘 선정 필요성이 요구된다.
의 시간 복잡도를 갖는다. 종종 데이크스트라 알고리즘과 자주 비교되곤 하는데, 두 알고리즘 모두 각각의 장단점이 있기 때문에 상황에 맞는 알고리즘 선정 필요성이 요구된다.
<자바 코드>
private static int N=5;public static void main(String[] args) {
// TODO Auto-generated method stub
int INF=999;
int D[][]=new int[N][N];
int M[][]=new int[N][N];
int W[][]=new int[N][N];
//D를 무한대로 입력
for(int row[]:D)
Arrays.fill(row, 999);
int i,j,k;
W=new int[][]{
{0,3,1,999,999},
{3,0,999,999,999},
{1,999,0,2,999},
{999,999,2,0,2},
{999,999,999,2,0}
};
for(i=0;i<N;i++)
{
for(j=0;j<N;j++){
D[i][j]=W[i][j];
}
}
for(i=0;i<N;i++)
{
for(j=0;j<N;j++)
{
for(k=0;k<N;k++){
if(D[j][k]>D[j][i]+D[i][k]){
D[j][k]=D[j][i]+D[i][k];
M[j][k]=i;
}
}
}
}
}
private static String floyd_warshall_path(int v1,int v2,int M[][])
{
Stack<Integer> S=new Stack<Integer>();
S.push(v2);
String P="";
while(M[v1][S.peek()]!=-1){
S.push(M[v1][S.peek()]);
}
while(!S.isEmpty())
{
P+=Integer.toString(S.peek());
S.pop();
}
return P;
}
참고: https://ko.wikipedia.org/wiki/플로이드-워셜_알고리즘

댓글
댓글 쓰기