(알고리즘) 피보나치 (재귀와 분할정복)

기존 피보나치의 수열을 구하는 알고리즘은 다음과 같다

?

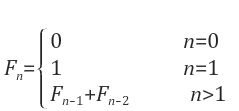
1 2 3 4 5 6 7 8

int Fibonacci(int n) { if(n==0) return 0; if(n==1 || n==2) return 1; return Fibonacci(n-1) + Fibonacci(n-2); }

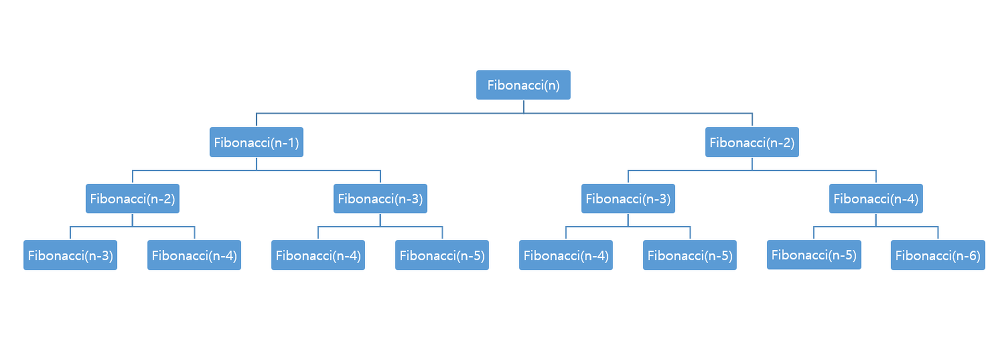하지만 이 알고리즘은 점점 재귀함수를 호출하는 횟수가 2배씩 늘어서

시간복잡도가 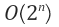이기 때문에 매우 비효율적이다.

하지만 행렬과 분할정복 기법을 활용하면 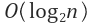 수준으로 알고리즘을 개선할 수 있다.

2) 동적계획법

//Fibonacci Series using Dynamic Programming

#include<stdio.h>

 

int fib(int n)

{

  /* Declare an array to store Fibonacci numbers. */

  int f[n+1];

  int i;

 

  /* 0th and 1st number of the series are 0 and 1*/

  f[0] = 0;

  f[1] = 1;

 

  for (i = 2; i <= n; i++)

  {

      /* Add the previous 2 numbers in the series

         and store it */

      f[i] = f[i-1] + f[i-2];

  }

 

  return f[n];

}




3)행렬 연산이용

This another O(n) which relies on the fact that if we n times multiply the matrix M = {{1,1},{1,0}} to itself (in other words calculate power(M, n )), then we get the (n+1)th Fibonacci number as the element at row and column (0, 0) in the resultant matrix.

The matrix representation gives the following closed expression for the Fibonacci numbers:

//Fibonacci Series using  Optimized Method class fibonacci {     /* function that returns nth Fibonacci number */     static int fib(int n)     {     int F[][] = new int[][]{{1,1},{1,0}};     if (n == 0)         return 0;     power(F, n-1);            return F[0][0];     }            static void multiply(int F[][], int M[][])     {     int x =  F[0][0]*M[0][0] + F[0][1]*M[1][0];     int y =  F[0][0]*M[0][1] + F[0][1]*M[1][1];     int z =  F[1][0]*M[0][0] + F[1][1]*M[1][0];     int w =  F[1][0]*M[0][1] + F[1][1]*M[1][1];           F[0][0] = x;     F[0][1] = y;     F[1][0] = z;     F[1][1] = w;     }            /* Optimized version of power() in method 4 */     static void power(int F[][], int n)     {     if( n == 0 || n == 1)       return;     int M[][] = new int[][]{{1,1},{1,0}};            power(F, n/2);     multiply(F, F);            if (n%2 != 0)        multiply(F, M);     }           /* Driver program to test above function */     public static void main (String args[])     {          int n = 9;      System.out.println(fib(n));     } } /* This code is contributed by Rajat Mishra */