(알고리즘) 라빈카프 알고리즘
*문자열 검색을 해시함수를 이용한다.
*패턴의 길이에 관계없이 본문의 길이에만 영향을 받는다.
*최초의 해시값(i가 0일때)는 구해야 한다.
*최초의 해시함수나 새 해시함수 모두 문자열의 길이가 늘어나면 해시값도 커진다는 문제점이있다. 따라서 해시값을 일정범위안에 가두기 위해 해시함수의 결과를 어느 값으로 나눈 나머지를 해시값으로 사용.
*패턴의 길이에 관계없이 본문의 길이에만 영향을 받는다.
*최초의 해시값(i가 0일때)는 구해야 한다.
*최초의 해시함수나 새 해시함수 모두 문자열의 길이가 늘어나면 해시값도 커진다는 문제점이있다. 따라서 해시값을 일정범위안에 가두기 위해 해시함수의 결과를 어느 값으로 나눈 나머지를 해시값으로 사용.
문자열의 길이가 4라고 할 때
한 칸 전진한 문자열은
H1은 H0를 이용하여 표현 할 수 있다.
H1은 다음과 같이 표현 할 수 있다.
Hi는 다음과 같이 나타낼 수 있다.
즉 i=0일때는 해시 값을 다 구해주고,
두번째, i>0일떄는 두 문자에만 접근한다.
<Code>
2^(m-1)은 coefficient로 변수로 두고 있다. 거듭제곱은 비용이 많이 소요되는 연산이기 때문이다. 게다가 한 패턴에 대해 2^(m-1)은 항상 같은 값으 가진다. 그래서 밖에서 계산한 후 안으로 가져와 사용하는 것이 훨씬 경제적이다.

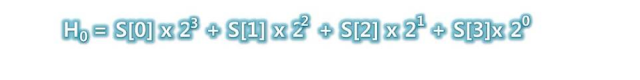









댓글
댓글 쓰기