(머신러닝) 4장. 나이브베이스: 확률 이론으로 분류하기
*나이브 베이스
장점: 소량의 데이터를 가지고 작업이 이루어지며, 여러 개의 분류 항목을 다룰 수 있다.
단점: 입력 데이터를 어떻게 준비하느냐에 따라 민감하게 작용한다.
적용: 명목형 값
1. 조건부확률
7개의 돌이 담긴 병이있다. 병 속의 돌중 3개는 회색 4개는 검은색이다. 이 병에 손을 넣고 임의로 돌 하나를 뽑는다면, 뽑은 돌이 회색일 가능성은 3/7이다.
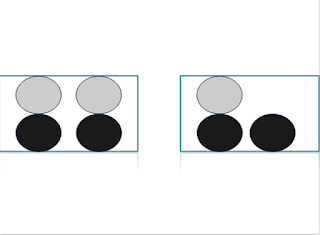
만약에 7개의 돌이 두 개의 양동이(bucket)에 있다면 어떻게 될까?
만약 P(회색) 나 P(검은색)을 계산하고자 한다면 양동이에 따라 답이 변하지 않겠는가?
만약 양동이 B에 회색 돌의 확률을 계산하고자 한다면, 아마도 회색 돌의 확률을 계산하는 방법을 알 수 있을 것이다. 이것을 조건부확률 이라고한다.
P(회색|bucketB)='양동이 B에 주어진 회색 돌의 확률'
이것은 1/3으로써,
P(회색|Bucket B)=P(회색 and Bucket B)/P(Bucket B)이다.==>(1/7)/(3/7)
조건부 확률을 다루기 위한 다른 유용한 방법으로 베이스 규칙이 있다.
만약에 P(x|c)를 알고 있는 상태에서 P(c|x)를 알기를 원한다면 다음과 같이 찾을 수 있다.
P(c|x)=(P(x|c)*P(c))/(P(x))
<나이브 베이스에 대한 일반적인 접근 방법>
1. 수집
2. 준비: 명목형 또는 부울형(Boolean)값이 요구된다.
3. 분석: 많은 속성들을 플롯 하는 것은 도움되지 못한다. 히스토그램으로 보는 것이 가장좋다.
4. 훈련: 각 속성을 독립적으로 조건부 확률을 계산한다.
5. 검사: 오류율을 계산한다.
*속성들이 서로 독립적이라고 가정하면, N^1000개의 데이터는 1000*N개로 줄어들게 된다. 독립이라는 것은 통계적인 독립을 의미한다. 즉, 하나의 속성 또는 단어가 다른 단어 옆에도 있는 가능성이 있다는 것이다. '베이컨'이 '맛있는' 이라는 단어 옆에 있을 가능성과 '건강에 해로운' 이라는 단어 옆에 나타날 가능성이 같다는 것이다. 물론, 이러한 가정은 참이 아니다.
이것은 나이브 베이스 분류기에서 나이브가 의미하는 것이다.
def trainNB0(trainMatrix,trainCategory):
numTrainDocs = len(trainMatrix)
numWords = len(trainMatrix[0])
pAbusive = sum(trainCategory)/float(numTrainDocs)
p0Num = ones(numWords); p1Num = ones(numWords) #change to ones()
p0Denom = 2.0; p1Denom = 2.0 #change to 2.0
for i in range(numTrainDocs):
if trainCategory[i] == 1:
p1Num += trainMatrix[i]
p1Denom += sum(trainMatrix[i])
else:
p0Num += trainMatrix[i]
p0Denom += sum(trainMatrix[i])
p1Vect = log(p1Num/p1Denom) #change to log()
p0Vect = log(p0Num/p0Denom) #change to log()
return p0Vect,p1Vect,pAbusive
--->위 함수는 문서 행렬인 trainMatrix와 각 문서에 대한 분류항목 trainCategory가 인자이다.
P(w0 | ci)와 P(w1 | ci) 를 계산하기 위해서 분자와 분모를 초기화 한다. p0Num , p1Num, p0Denom, p1Denom이 해당한다.
많은 w들을 가지고 빠르게 계산하기 위해 Numpy의 배열을 사용하게 될 것이다. 분자는 Numpy의 배열로 표현되며, 배열의 크기는 마치 어휘집 내에 가지고 있는 단어들처럼 원소의 갯수와 같다. 반복문에서는 trainMatrix나 훈련 집합에 있는 모든 문서를 반복한다. 반복을 할때마다 하나의 단어는 하나의 문서 내에 나타나게 되며, 이때마다 단어의 개수(p1Num 또는 p0Num)는 증가한다.
문서분류를 시작할 때, 주어진 분류항목의 속하는 문서의 확률을 구하기 위해 많은 양의 확률들을 가지고 곱하기를 한다. P(w0 | ci)*P(w1 | ci)*......P(wN | ci)와 같이 표시된다. 이 숫자중 하나가 0이라면, 이것과 함께 다른 것들을 곱할 경우 0을 얻게된다. 이러한 영향력을 줄이기 위해 단어의 갯수를 모두 1로초기화하고 분모는 2로 초기화한다.
다른문제로 언더플로우(underflow)가 있다. 이 문제는 작은 수끼리 너무 많이 곱해져서 발생하는 문제이다. P(w0 | ci)*P(w1 | ci)*......P(wN | ci)처럼 매우 작은 수들을 많이 곱할떄 언더플로우가 발생하거나 부정확한 답을 산출하게 된다.
이러한 문제를 해결하기 위한 한 가지 방법은 이 산출 결과에 대해 자연로그를 계산하는 것이다. ln(a*b)=ln(a)+ln(b)와 같다.
산출결과에 자연로그를 사용하면 산출 결과의 원래 의미가 상실되지 않을까? 답은 아니오다. 함수 f(x)와 ln(f(x))의 플롯을 검토해보면 같은 영역에서 증가하고 줄어들며, 같은 지점에서 최고점을 찍는다는 것을 확인할 수 있을 것이다.
def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
p1 = sum(vec2Classify * p1Vec) + log(pClass1) #element-wise mult
p0 = sum(vec2Classify * p0Vec) + log(1.0 - pClass1)
if p1 > p0:
return 1
else:
return 0
--->위 코드는 네 개의 입력 변수를 받는다. 하나는 vec2Classify라는 분류를 위한 벡터이고 나머지 세개는 함수 trainNB0()에서 계산된 확률이다. 우리는 두 벡터를 곱하기 위해 Numpy의 배열을 사용한다.
원소들을 곱하는 방식은 두 벡터의 첫 번째 원소들을 곱한뒤, 두 번쨰 원소들을 곱하고, 이런식으로 계속해서 끝까지 곱해가는 방식이다. 그런 다음, 어휘집에 있는 모든 단어들에 대한 값을 더하고, 분류 항목의 로그확률에 더한다.
2.4 준비: 중복 단어 문서 모델
하나의 문서 내에 하나의 단어가 한 번 이상 나타난다면 ,문서에 관한 정보의 유형, 즉 단지 문서에서 단어가 발생하는지 그렇지 않은지를 전달하게 될 것이다. 이러한 접근 방법을 중복 단어 모델(the bag-of-words)이라고 한다.
*나이브 베이스 중복 단어 모델
def bagOfWords2VecMN(vocabList, inputSet):
returnVec = [0]*len(vocabList)
for word in inputSet:
if word in vocabList:
returnVec[vocabList.index(word)] += 1
return returnVec
장점: 소량의 데이터를 가지고 작업이 이루어지며, 여러 개의 분류 항목을 다룰 수 있다.
단점: 입력 데이터를 어떻게 준비하느냐에 따라 민감하게 작용한다.
적용: 명목형 값
1. 조건부확률
7개의 돌이 담긴 병이있다. 병 속의 돌중 3개는 회색 4개는 검은색이다. 이 병에 손을 넣고 임의로 돌 하나를 뽑는다면, 뽑은 돌이 회색일 가능성은 3/7이다.
만약에 7개의 돌이 두 개의 양동이(bucket)에 있다면 어떻게 될까?
만약 P(회색) 나 P(검은색)을 계산하고자 한다면 양동이에 따라 답이 변하지 않겠는가?
만약 양동이 B에 회색 돌의 확률을 계산하고자 한다면, 아마도 회색 돌의 확률을 계산하는 방법을 알 수 있을 것이다. 이것을 조건부확률 이라고한다.
P(회색|bucketB)='양동이 B에 주어진 회색 돌의 확률'
이것은 1/3으로써,
P(회색|Bucket B)=P(회색 and Bucket B)/P(Bucket B)이다.==>(1/7)/(3/7)
조건부 확률을 다루기 위한 다른 유용한 방법으로 베이스 규칙이 있다.
만약에 P(x|c)를 알고 있는 상태에서 P(c|x)를 알기를 원한다면 다음과 같이 찾을 수 있다.
P(c|x)=(P(x|c)*P(c))/(P(x))
<나이브 베이스에 대한 일반적인 접근 방법>
1. 수집
2. 준비: 명목형 또는 부울형(Boolean)값이 요구된다.
3. 분석: 많은 속성들을 플롯 하는 것은 도움되지 못한다. 히스토그램으로 보는 것이 가장좋다.
4. 훈련: 각 속성을 독립적으로 조건부 확률을 계산한다.
5. 검사: 오류율을 계산한다.
*속성들이 서로 독립적이라고 가정하면, N^1000개의 데이터는 1000*N개로 줄어들게 된다. 독립이라는 것은 통계적인 독립을 의미한다. 즉, 하나의 속성 또는 단어가 다른 단어 옆에도 있는 가능성이 있다는 것이다. '베이컨'이 '맛있는' 이라는 단어 옆에 있을 가능성과 '건강에 해로운' 이라는 단어 옆에 나타날 가능성이 같다는 것이다. 물론, 이러한 가정은 참이 아니다.
이것은 나이브 베이스 분류기에서 나이브가 의미하는 것이다.
2. 파이썬으로 텍스트 분류하기.
2.1 준비: 텍스트로 단어 벡터 만들기
def createVocabList(dataSet):
vocabSet = set([]) #create empty set
for document in dataSet:
vocabSet = vocabSet | set(document) #union of the two sets
return list(vocabSet)
--->유일한 단어 목록을 생성한다. 이떄,집합 자료구조를 사용한다. 먼저, 아무것도 저장되지 않은 빈 집합 유형의 변수를 생성한다. 그런다음, 이 변수에 각 문서로부터 새로운 집합 유형의 변수를생성하여 첨부한다. 연산자 | 는 두개의 집합 유형의 변수를 합치는데 사용하는 연산자다.
def setOfWords2Vec(vocabList, inputSet):
returnVec = [0]*len(vocabList)
for word in inputSet:
if word in vocabList:
returnVec[vocabList.index(word)] = 1
else: print "the word: %s is not in my Vocabulary!" % word
return returnVec
---->이 함수는 주어진 문서 내에 어휘 목록에 있는 단어가 존재하는지 아닌지를 표현하기 위해 어휘목록, 문서, 1과0의 출력벡터를 사용한다. 어휘목록과 같은 길이의 벡터를 생성하고 모두 0으로 채운다. 그 다음, 문서 내에 있는 단어를 하나하나 비교한다. 그러다가 단어가 어휘목록에있으면 단어의 값을 1로 설정한다.
2.2 훈련: 단어 벡터로 학률 계산하기
P(ci | w)= (P(w | ci)*P(ci))/P(w)
여기서 w는 어휘집에있는 단어들이다.
P(ci)는 i번째 분류항목(폭력적인 글인지 아니면 폭력적이지 않은 글인지)을 나타낸다.
그럼 P(w | ci)는 어떻게 구할까?
이것은 나이브 가정에서 찾을 수 있다. w를 개별적인 속성으로 펼치면, P(w0,w1,w2... | ci)처럼 다시 쓸 수 있다. 여기서 우리는 모든 단어들이 서로 독립적이라고 가정하며 이를 조건부 독립이라고 한다. 이에 대한 확률은 P(w0 | ci)*P(w1 | ci)*......P(wN | ci)로 쉽게 계산된다.
def trainNB0(trainMatrix,trainCategory):
numTrainDocs = len(trainMatrix)
numWords = len(trainMatrix[0])
pAbusive = sum(trainCategory)/float(numTrainDocs)
p0Num = ones(numWords); p1Num = ones(numWords) #change to ones()
p0Denom = 2.0; p1Denom = 2.0 #change to 2.0
for i in range(numTrainDocs):
if trainCategory[i] == 1:
p1Num += trainMatrix[i]
p1Denom += sum(trainMatrix[i])
else:
p0Num += trainMatrix[i]
p0Denom += sum(trainMatrix[i])
p1Vect = log(p1Num/p1Denom) #change to log()
p0Vect = log(p0Num/p0Denom) #change to log()
return p0Vect,p1Vect,pAbusive
--->위 함수는 문서 행렬인 trainMatrix와 각 문서에 대한 분류항목 trainCategory가 인자이다.
P(w0 | ci)와 P(w1 | ci) 를 계산하기 위해서 분자와 분모를 초기화 한다. p0Num , p1Num, p0Denom, p1Denom이 해당한다.
많은 w들을 가지고 빠르게 계산하기 위해 Numpy의 배열을 사용하게 될 것이다. 분자는 Numpy의 배열로 표현되며, 배열의 크기는 마치 어휘집 내에 가지고 있는 단어들처럼 원소의 갯수와 같다. 반복문에서는 trainMatrix나 훈련 집합에 있는 모든 문서를 반복한다. 반복을 할때마다 하나의 단어는 하나의 문서 내에 나타나게 되며, 이때마다 단어의 개수(p1Num 또는 p0Num)는 증가한다.
문서분류를 시작할 때, 주어진 분류항목의 속하는 문서의 확률을 구하기 위해 많은 양의 확률들을 가지고 곱하기를 한다. P(w0 | ci)*P(w1 | ci)*......P(wN | ci)와 같이 표시된다. 이 숫자중 하나가 0이라면, 이것과 함께 다른 것들을 곱할 경우 0을 얻게된다. 이러한 영향력을 줄이기 위해 단어의 갯수를 모두 1로초기화하고 분모는 2로 초기화한다.
다른문제로 언더플로우(underflow)가 있다. 이 문제는 작은 수끼리 너무 많이 곱해져서 발생하는 문제이다. P(w0 | ci)*P(w1 | ci)*......P(wN | ci)처럼 매우 작은 수들을 많이 곱할떄 언더플로우가 발생하거나 부정확한 답을 산출하게 된다.
이러한 문제를 해결하기 위한 한 가지 방법은 이 산출 결과에 대해 자연로그를 계산하는 것이다. ln(a*b)=ln(a)+ln(b)와 같다.
산출결과에 자연로그를 사용하면 산출 결과의 원래 의미가 상실되지 않을까? 답은 아니오다. 함수 f(x)와 ln(f(x))의 플롯을 검토해보면 같은 영역에서 증가하고 줄어들며, 같은 지점에서 최고점을 찍는다는 것을 확인할 수 있을 것이다.
def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
p1 = sum(vec2Classify * p1Vec) + log(pClass1) #element-wise mult
p0 = sum(vec2Classify * p0Vec) + log(1.0 - pClass1)
if p1 > p0:
return 1
else:
return 0
--->위 코드는 네 개의 입력 변수를 받는다. 하나는 vec2Classify라는 분류를 위한 벡터이고 나머지 세개는 함수 trainNB0()에서 계산된 확률이다. 우리는 두 벡터를 곱하기 위해 Numpy의 배열을 사용한다.
원소들을 곱하는 방식은 두 벡터의 첫 번째 원소들을 곱한뒤, 두 번쨰 원소들을 곱하고, 이런식으로 계속해서 끝까지 곱해가는 방식이다. 그런 다음, 어휘집에 있는 모든 단어들에 대한 값을 더하고, 분류 항목의 로그확률에 더한다.
2.4 준비: 중복 단어 문서 모델
하나의 문서 내에 하나의 단어가 한 번 이상 나타난다면 ,문서에 관한 정보의 유형, 즉 단지 문서에서 단어가 발생하는지 그렇지 않은지를 전달하게 될 것이다. 이러한 접근 방법을 중복 단어 모델(the bag-of-words)이라고 한다.
*나이브 베이스 중복 단어 모델
def bagOfWords2VecMN(vocabList, inputSet):
returnVec = [0]*len(vocabList)
for word in inputSet:
if word in vocabList:
returnVec[vocabList.index(word)] += 1
return returnVec

댓글
댓글 쓰기